Изображение к статье создано при помощи нейросети Kandinsky
Всем привет.
О том, как очень просто и быстро найти середину отрезка, описано, в частности, здесь: https://ru.wikihow.com/найти-середину-отрезка-прямой
В сегодняшней статье я расскажу о том, как найти и нарисовать центр линии на языке C# в приложении Windows Forms, используя для рисования доступные возможности и средства GDI+. В данный момент я разрабатываю одну программу для визуального проектирования игровых объектов 2D-игр, и в этой программе мне потребовалась реализация функционала "Линейка", который бы измерял расстояние между двумя точками линии, нарисованной на форме в приложении Windows Forms, а также находил бы центральную точку линии (отрезка между двумя заданными точками).
Поскольку нет известных и штатных средств найти/нарисовать центр линии, мне потребовалось это сделать вручную, при помощи использования формул, знакомых нам из курса средней школы: в данной задаче нам очень поможет теорема Пифагора, а также тригонометрические функции (конкретно в нашем примере нам потребуется найти косинус угла).
Если вы ещё не сталкивались с GDI+, то рекомендую перед этой статьёй прочитать другую мою вводную статью "Рисуем фигуры на C# при помощи средств GDI+" по отрисовке простых фигур средствами GDI+, где я кратко рассказываю про этот стандартный интерфейс графического устройства, предоставляю внешние ссылки по этой теме и объясняю, как рисовать различные фигуры на форме в приложении Windows Forms.
Итак, в контексте этой статьи мы напишем с вами программу для Windows Forms, в которой будем строить и рисовать линию по двум заданным нами точкам, а также находить центральную точку этой линии. Мы также будем выводить координаты X и Y для всех точек отрисованной линии: для граничных точек и центральной точки, координаты которой мы рассчитаем специальным образом при помощи упомянутой теоремы Пифагора и тригонометрической функции Cos (косинус).
В конце статьи, как обычно, я дам ссылку на архив с готовым проектом для среды Microsoft Visual Studio, который мы напишем в этой статье.
Давайте сразу посмотрим на то, как будет выглядеть разрабатываемая нами программа.
При запуске программа начнёт отслеживать движение курсора мыши и рисовать небольшую окружность - в месте центра курсора. А также выводить текущие координаты точки, соответствующей положению курсора мыши:
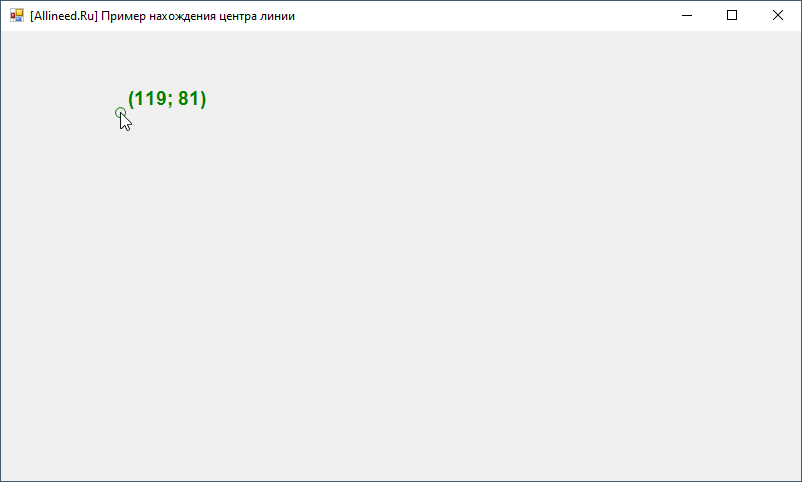
Пока мы будем двигать курсором в области формы, мы тем самым будем выбирать начальную точку нашей линии. Для фиксации начальной точки линии нужно будет кликнуть по форме левой кнопкой мыши.
Как только начальная точка линии нами зафиксирована, она станет закрашенным красным кругом (также будут выводиться координаты этой 1-й точки), а при дальнейшем движении курсора мыши в области формы мы будем выводить разметочную линию, говорящую нам о том, как именно будет построена линия с учётом выбора 2-й точки линии. В этот же момент мы будем динамически рассчитывать центр этого отрезка (т.е. центральную точку линии) и также выводить её в виде оранжевой окружности вместе с её координатами (шрифтом оранжевого цвета):
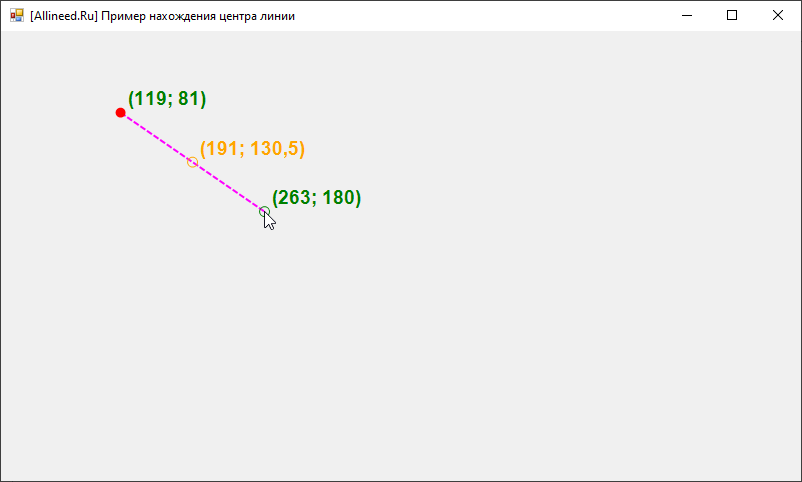
Мы сможем как угодно выбирать 2-ю точку линии на форме, и при этом центральная точка всегда будет также динамически рассчитана и отображена вместе с её координатами:
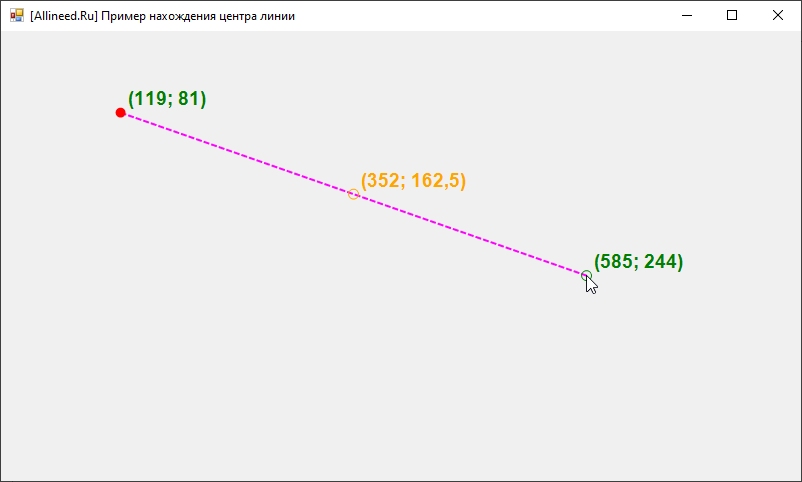
Когда мы захотим зафиксировать нашу линию, мы снова кликнем по форме второй раз, в итоге линия будет жёстко зафиксирована вместе с её центральной точкой и координатами всех трёх точек:

После фиксации линии на форме мы отобразим подсказку - текст "Клик правой кнопкой мыши - сброс измерений и начать заново". Начальная точка линии будет в виде красного круга, конечная точка линии - в виде синего круга, а центральная - в виде оранжевого круга. Когда мы кликнем правой кнопкой мыши в любой области формы, то измерение начнётся заново: мы вновь будем находиться в состоянии выбора первой точки линии. И так процесс может повторяться вновь и вновь.
Давайте приступим к реализации такой программы.
Создание нового проекта в среде Microsoft Visual Studio
Откройте среду разработки Microsoft Visual Studio и создайте новый проект с типом Приложение Windows Forms (.NET Framework), как показано ниже:
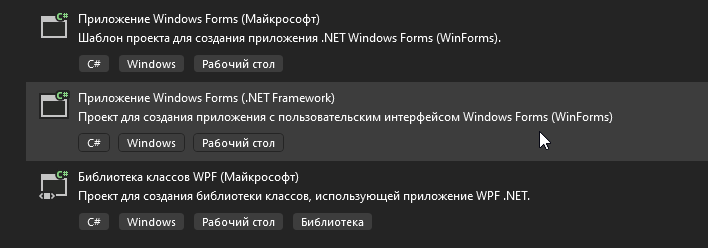
В качестве имени нового проекта задайте GDIFindCenterOfLineExample и выберите местоположение, куда будут сохранены файлы нового проекта (здесь я обычно оставляю все настройки по умолчанию и рекомендую сделать то же самое, просто запомните каталог, указанный в поле "Расположение", чтобы затем открывать его в Проводнике).
Переименование главной формы приложения
После создания проекта будет создана главная форма по умолчанию с именем Form1 и соответствующий ей файл, содержащий код для класса формы, с именем Form1.cs.
Выберем в окне "Обозреватель решений" эту форму и в окне "Свойства" изменим название класса для формы на FrmFindCenterOfLine.cs.
В диалоговом окне, запрашивающем подтверждение переименования класса формы и связанных с ней файлов, соглашаемся. В результате этих действий в окне "Обозреватель решений" форма и зависящие от неё файлы будут переименованы.
Теперь установим главной форме значения для некоторых её свойств.
Установка свойств для главной формы приложения
В окне "Свойства" для главной формы установим следующие значения свойств:
- Text - [Allineed.Ru] Пример нахождения центра линии
- Size - 816; 489
- StartPosition - CenterScreen
Все остальные свойства главной формы нашего приложения оставим с их значениями по умолчанию.
Теперь перейдем непосредственно к основной части - реализации логики программы.
Пишем код для главной формы
Дважды кликнем по главной форме из области конструктора. В результате для нас сгенерируется метод-обработчик для события загрузки формы (Load). Добавим в него следующую строку, которая включает двойную буферизацию для более плавной отрисовки объектов на форме и исключения эффекта "мерцания":
private void FrmFindCenterOfLine_Load(object sender, EventArgs e) {
this.DoubleBuffered = true;
}Следующим шагом в самом верху кода формы мы удалим все импорты, кроме следующих трёх, которые нам будут нужны для нашего приложения:
using System;
using System.Drawing;
using System.Windows.Forms;Теперь зададим в классе формы следующий enum-тип LinePaintingState, закрытую переменную класса CurrentLinePaintingState этого enum-типа и два закрытых (private) поля FirstLinePoint и SecondLinePoint, которые будут хранить координаты 1-й и 2-й точек линии:
/// <summary>
/// Перечисление задаёт состояние отрисовки линии
/// </summary>
public enum LinePaintingState {
/// <summary>
/// Состояние: "Выбираем 1-ю точку линии"
/// </summary>
ChoosingFirstPoint,
/// <summary>
/// Состояние: "Выбираем 2-ю точку линии"
/// </summary>
ChoosingSecondPoint,
/// <summary>
/// Состояние: "Ожидаем сброса результатов измерений"
/// </summary>
WaitingForReset
}
/// <summary>
/// Текущее состояние отрисовки линии. По умолчанию - "Выбираем 1-ю точку линии"
/// </summary>
private LinePaintingState CurrentLinePaintingState = LinePaintingState.ChoosingFirstPoint;
/// <summary>
/// Первая точка рисуемой линии
/// </summary>
private Point FirstLinePoint { get; set; } = Point.Empty;
/// <summary>
/// Вторая точка рисуемой линии
/// </summary>
private Point SecondLinePoint { get; set; } = Point.Empty;Перечисляемый тип LinePaintingState задаёт возможные состояния при отрисовке линии:
- ChoosingFirstPoint - мы в состоянии выбора первой точки линии
- ChoosingSecondPoint - мы в состоянии выбора второй точки линии. При этом 1-я точка линии была уже зафиксирована в переменной FirstLinePoint вместе с её координатами, когда мы находились в состоянии ChoosingFirstPoint
- WaitingForReset - обе точки линии зафиксированы - первая в переменной FirstLinePoint, вторая - в переменной SecondLinePoint, а также произведено вычисление координат центральной точки линии
Переменная CurrentLinePaintingState исходно выставлена в значение состояния LinePaintingState.ChoosingFirstPoint, что говорит о том, что при старте приложения мы сразу находимся на шаге выбора 1-й точки линии.
Теперь перейдём к представлению визуального конструктора главной формы и в окне "Свойства" среды разработки найдём иконку с изображением "молнии". Кликнем по ней, чтобы перейти к доступным для обработки событиям формы.
Нам будет нужно обработать следующие события для главной формы:
- MouseDown - событие нажатия кнопки мыши на форме, когда курсор мыши находится над областью формы
- MouseMove - событие, возникающее при движении курсора мыши над областью формы
- Paint - событие, вызываемое при необходимости перерисовки элемента управления (в нашем случае - главной формы).
- Load - для него мы уже написали код выше и включили свойство DoubleBuffer для формы.
Для создания методов-обработчиков для указанных событий (кроме события Load, т.к. его мы уже обработали) - дважды кликаем левой кнопкой мыши напротив каждого события, в результате будет создаваться обработчик для этого события. Повторяем операцию, пока не будут созданы пустые методы-обработчики для всех трёх событий MouseDown, MouseMove и Paint:
private void FrmFindCenterOfLine_MouseDown(object sender, MouseEventArgs e) {
}
private void FrmFindCenterOfLine_MouseMove(object sender, MouseEventArgs e) {
}
private void FrmFindCenterOfLine_Paint(object sender, PaintEventArgs e) {
}Напишем следующую реализацию для метода-обработчика события MouseDown, т.е. заполним первый из пустых сгенерированных методов следующим образом:
/// <summary>
/// Обработка события нажатия кнопки мыши на форме, когда курсор мыши находится над областью формы
/// </summary>
/// <param name="sender">объект, отправивший событие (экземпляр главной формы)</param>
/// <param name="e">экземпляр класса MouseEventArgs, содержащий параметры вызванного события</param>
private void FrmFindCenterOfLine_MouseDown(object sender, MouseEventArgs e) {
if (e.Button == MouseButtons.Left) {
// произведён клик левой кнопкой мыши по области формы
switch (CurrentLinePaintingState) {
case LinePaintingState.ChoosingFirstPoint:
// запоминаем местоположение первой точки линии
FirstLinePoint = e.Location;
// изменяем состояние отрисовки линии на "Выбор 2-й точки линии"
CurrentLinePaintingState = LinePaintingState.ChoosingSecondPoint;
break;
case LinePaintingState.ChoosingSecondPoint:
// запоминаем местоположение второй точки линии
SecondLinePoint = e.Location;
// изменяем состояние отрисовки линии на "Ожидание сброса"
CurrentLinePaintingState = LinePaintingState.WaitingForReset;
// принудительно перерисовываем форму
Invalidate();
break;
}
} else if (e.Button == MouseButtons.Right) {
switch (CurrentLinePaintingState) {
case LinePaintingState.WaitingForReset:
CurrentLinePaintingState = LinePaintingState.ChoosingFirstPoint;
break;
}
}
}Код метода содержит основное условие, которое проверяет, какая из кнопок мыши была нажата. Если левая кнопка, то мы проверяем текущее состояние рисования линии (т.е. значение переменной CurrentLinePaintingState), и в случае, если мы выбирали первую точку линии (LinePaintingState.ChoosingFirstPoint), то мы сохраняем её координаты в переменную FirstLinePoint. Если же клик левой кнопкой мыши был в момент, когда производился выбор второй точки линии, то мы сохраняем координаты курсора мыши (e.Location) в момент клика в переменную SecondLinePoint. В обоих случаях мы изменяем значение переменной CurrentLinePaintingState на следующее.
Аналогичным образом при клике правой кнопкой мыши (развилка else if в коде метода) мы проверяем, что находились в состоянии LinePaintingState.WaitingForReset, т.е. ожидали сброса результатов измерения линии. И при клике мышью в этом случае мы возвращаемся в исходное состояние, присваивая переменной CurrentLinePaintingState значение LinePaintingState.ChoosingFirstPoint, т.е. мы снова находимся в выборе первой точки линии.
Теперь давайте реализуем обработку события MouseMove. Метод-обработчик для этого события будет содержать всего несколько строк кода:
private void FrmFindCenterOfLine_MouseMove(object sender, MouseEventArgs e) {
if (CurrentLinePaintingState != LinePaintingState.WaitingForReset) {
Invalidate();
}
}Этот код означает следующее: пока мы находимся не в состоянии ожидания сброса результатов измерений, т.е. пока переменная класса CurrentLinePaintingState не равна LinePaintingState.WaitingForReset, мы будем при каждом движении мышью над областью формы вызывать метод Invalidate(), который приводит к перерисовке области формы, т.е. приводит к генерации события Paint, а значит, и к вызову метода-обработчика для события Paint, заготовку кода для которого мы сейчас напишем. Т.е. фактически при движении мышью над областью формы мы будем постоянно перерисовывать форму, с учётом положения 1-й точки и положения курсора мыши над формой, получая при этом динамически изменяющуюся картину расположения 1-й точки, курсора мыши, линии их соединяющей и центральной точки линии на нашей главной форме. Как именно мы получим это поведение мы узнаем чуть далее.
Теперь настало время написать код для третьего метода-обработчика для события Paint. Однако полностью код этого метода мы пока написать не сможем, поскольку нам не хватает вспомогательных служебных методов, которые будут осуществлять отрисовку различных объектов. Поэтому мы напишем код метода лишь частично, а затем, когда эти служебные методы также будут нами реализованы, вернёмся снова к коду обработчика для события Paint и допишем необходимые участки кода.
Итак, давайте для обработки события Paint напишем следующий начальный код, который будет пока основой нашей логике по отрисовке объектов на форме:
private void FrmFindCenterOfLine_Paint(object sender, PaintEventArgs e) {
Graphics g = e.Graphics;
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.HighQuality;
switch (CurrentLinePaintingState) {
case LinePaintingState.ChoosingFirstPoint:
// TODO: выполнить действия по отрисовке формы, когда мы находимся в состоянии выбора 1-й точки линии
break;
case LinePaintingState.ChoosingSecondPoint:
// TODO: выполнить действия по отрисовке формы, когда мы находимся в состоянии выбора 2-й точки линии
break;
case LinePaintingState.WaitingForReset:
// TODO: выполнить действия по отрисовке формы, когда мы находимся в состоянии ожидания сброса результатов измерений (т.е. когда обе точке линии нам известны, линия полностью готова, а также отрисована центральная точка линии
break;
}
}Давайте разберём данную заготовку кода и каркас нашей логики. В первой строке кода мы определяем собственную переменную класса Graphics с именем g и записываем в неё готовый экземпляр класса Graphics, который можно использовать для рисования на форме. Этот готовый экземпляр всегда приходит в параметрах события Paint и доступен через 2-й параметр e с типом PaintEventArgs.
Далее мы сразу устанавливаем режим сглаживания (SmoothingMode), который также разбирали уже в статье "Рисуем фигуры на C# при помощи средств GDI+", поэтому скажу лишь кратко, что он позволяет добиться лучшего сглаживания нарисованных на форме объектов/фигур и избежать углов с "засечками".
Следом идёт оператор switch, которым мы будем проверять текущее состояние отрисовки нашей линии: на каждое из возможных значений нашего enum-типа LinePaintingState выставлены ветки case. Но, как видите, мы пока не готовы написать код этих веток case, а оставили лишь TODO-комментарии с заметками о том, что мы собираемся делать при обработке каждого случая case.
Дальше мы перейдем к написанию служебных вспомогательных методов для рисования объектов, которые мы постепенно будем добавлять в каждую развилку case. И в конце мы получим полностью готовый код для обработки события Paint.
Пишем служебные вспомогательные методы для отрисовки объектов
Начнём мы с написания метода GetMouseCursorPositionInClientCoordinates(), который не будет принимать никаких входных параметров и будет возвращать экземпляр класса Point. Задача этого метода будет простой: он должен получить текущее местоположение курсора мыши в координатах экрана и перевести эти экранные координаты в клиентские координаты. Разница между этими двумя типами координат следующая: экранные координаты хранят местоположение (т.е. значения координат X и Y) курсора мыши относительно экрана. Очевидно, что экран всегда больше, чем область главной формы нашего приложения, а нас интересует, где именно в пределах формы находится курсор мыши в данный момент времени. Клиентские же координаты - это как раз местоположение курсора мыши относительного левого-верхнего края главной формы. Поэтому для перевода координат из экранных в клиентские мы используем доступный метод PointToClient, передавая ему экранные координаты курсора мыши:
/// <summary>
/// Метод возвращает экземпляр класса Point, хранящий координаты X и Y курсора мыши
/// в клиентских координатах.
/// </summary>
/// <returns>экземпляр класса Point, хранящий клиентские координаты курсора мыши</returns>
private Point GetMouseCursorPositionInClientCoordinates() {
Point mouseCursorPosition = Cursor.Position;
return this.PointToClient(mouseCursorPosition);
}Отлично, первый вспомогательный метод уже готов, и мы идём далее. Напишем в коде главной формы также следующий метод DrawLinePoint(Graphics g, Point point, Brush brush):
/// <summary>
/// Метод рисует на форме круг диаметром 10 пикселей с заданным при помощи параметра кисти <paramref name="brush"/> цветом.
/// Параметр <paramref name="point"/> определяет точку на форме, которая будет являться центром этого круга.
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки круга</param>
/// <param name="point">экземпляр класса Point, определяющий центральную точку круга</param>
/// <param name="brush">кисть, которую необходимо использовать для заливки круга</param>
private void DrawLinePoint(Graphics g, Point point, Brush brush) {
g.FillEllipse(brush, new Rectangle(point.X - 5, point.Y - 5, 10, 10));
}Этот метод принимает три параметра: в первом параметре g мы будем передавать методу инициализированный экземпляр класса Graphics, который у нас уже был получен в методе-обработчике события Paint. Во втором параметре point будем передавать точку, которая будет являться центром круга, а сам круг будет являться визуальным представлением на главной форме какой-либо точки рисуемой линии. В третьем параметре brush мы будем передавать "кисть" (Brush), которой нужно закрасить рисуемый круг, т.е. точку нашей линии. В единственной строке кода метода мы вызываем метод FillEllipse, который предназначается для рисования закрашенных эллипсов (или окружностей). В него мы передаем кисть из входного параметра метода, а также экземпляр прямоугольника (Rectangle), который будет являться описанным вокруг эллипса/окружности. Экземпляр прямоугольника мы создаём с одинаковыми значениями для ширины и высоты, равными 10 пикселей, а значит, наш прямоугольник будет являться квадратом, а эллипс, вписанный в него, на самом деле будет являться правильной окружностью (т.к. эллипс вписанный в квадрат - это окружность). От координат X и Y переданной точки point мы отнимаем по 5 пикселей, тем самым получая смещение влево-вверх для той точки, которая будет являться верхней-левой точкой нашего описанного вокруг окружности квадрата. Также помним из статьи "Рисуем фигуры на C# при помощи средств GDI+", что Fill-методы GDI+ рисуют заполненные фигуры, а значит, при отрисовке на форме мы получим в итоге не окружность, а закрашенный нужной нам "кистью" круг.
Теперь нам нужно будет написать вспомогательный метод для рисования разметочной штриховой линии, которая будет проходить от 1-й точки рисуемой нами линии до какой-то целевой точки targetPoint:
/// <summary>
/// Метод рисует линию от первой точки линии до другой целевой точки <paramref name="targetPoint"/>.
/// В состоянии выбора 2-й точки линии целевой точкой будет являться местоположение курсора мыши.
/// В состоянии полностью готовой линии целевой точкой будет являться непосредственно 2-я точка линии.
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки линии</param>
/// <param name="targetPoint">целевая точка, до которой нужно нарисовать линию от первой точки линии</param>
private void DrawLineFromFirstPointToOtherPoint(Graphics g, Point targetPoint) {
Pen dashedMagentaPen = new Pen(Brushes.Magenta, 2);
dashedMagentaPen.DashStyle = System.Drawing.Drawing2D.DashStyle.Dash;
g.DrawLine(dashedMagentaPen, FirstLinePoint, targetPoint);
dashedMagentaPen.Dispose();
}Добавим его также к коду главной формы и разберём, что он делает. В первой строке метода мы создаём экземпляр "ручки" (Pen) в переменной dashedMagentaPen. Для цвета ручки мы используем готовую кисть из Brushes.Magenta, а также устанавливаем толщину линии в 2 пикселя (2-й аргумент для конструктора при создании экземпляра класса Pen).
Дополнительно мы устанавливаем нашему экземпляру "ручки" значение стиля штриха, присваивая свойству DashStyle значение System.Drawing.Drawing2D.DashStyle.Dash, т.е. наша линия будет не сплошной, а штриховой.
Следом мы рисуем саму линию, вызывая метод GDI+ с именем DrawLine у экземпляра g класса Graphics, и передаём ей параметры: созданную "ручку" (dashedMagentaPen), первую точку нашей основной линии (FirstLinePoint), а также ту целевую точку targetPoint, которую наш вспомогательный метод будет принимать в параметре.
В конце метода мы освобождаем ресурсы, занимаемые экземпляром созданной "ручки" dashedMagentaPen, вызывая у него метод Dispose(). На этом наш новый метод полностью готов, и позже мы его обязательно используем по назначению.
Теперь напишем в коде главной формы следующий метод DrawCircleForMouseCursor(Graphics g, Point mouseCursorPositionClient):
/// <summary>
/// Рисует окружность зелёного цвета и диаметром 10 пикселей в той точке, где находится курсор мыши
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки окружности</param>
/// <param name="mouseCursorPositionClient">точка, задающая местоположение курсора мыши в клиентских координатах</param>
private void DrawCircleForMouseCursor(Graphics g, Point mouseCursorPositionClient) {
g.DrawEllipse(Pens.Green, new Rectangle(mouseCursorPositionClient.X - 5, mouseCursorPositionClient.Y - 5, 10, 10));
}Этот метод нарисует окружность зелёного цвета в той точке, которая в данный момент является местоположение курсора мыши, в клиентских координатах. Эта точка - второй параметр mouseCursorPositionClient нашего метода. Единственная строка кода в методе не нуждается в особых пояснениях, она просто рисует окружность диаметром 10 пикселей в точке курсора мыши, очень похожее мы уже делали с вами выше, реализуя метод DrawLinePoint, только там мы рисовали закрашенный круг, а здесь рисуем окружность без заливки.
Мы также хотим выводить координаты возле рисуемых точек линии, поэтому давайте напишем метод, который будет отвечать за данную задачу и назовём его DrawCoordinatesForPoint(Graphics g, PointF point, Brush brush):
/// <summary>
/// Рисует текст с координатами заданной точки <paramref name="point"/> и использует экземпляр
/// кисти <paramref name="brush"/> для указания цвета для шрифта.
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки текста</param>
/// <param name="point">экземпляр точки, для которой необходимо вывести текст с её координатами</param>
/// <param name="brush">экземпляр кисти, который задаёт цвет для рисования текста</param>
private void DrawCoordinatesForPoint(Graphics g, PointF point, Brush brush) {
string mouseCursorCoordinates = string.Format("({0}; {1})", point.X, point.Y);
Font mouseCursorCoordinatesFont = new Font("Arial", 14, FontStyle.Bold);
SizeF textSize = g.MeasureString(mouseCursorCoordinates, mouseCursorCoordinatesFont);
Color bgColorForBrush = Color.FromArgb(210, BackColor.R, BackColor.G, BackColor.B);
Brush brushForTextBackground = new SolidBrush(bgColorForBrush);
g.FillRectangle(brushForTextBackground, new RectangleF(new PointF(point.X + 5, point.Y - 25), new SizeF(textSize.Width, textSize.Height)));
g.DrawString(mouseCursorCoordinates, mouseCursorCoordinatesFont, brush, new PointF(point.X + 5, point.Y - 25));
mouseCursorCoordinatesFont.Dispose();
brushForTextBackground.Dispose();
}Я предоставил документацию на метод, поэтому параметры метода пояснять отдельно не буду. А по логике кода этого метода давайте сделаем небольшой разбор.
В первой строке метода в переменную mouseCursorCoordinates мы записываем строку с использованием метода Format, доступного для встроенного типа данных string. Можно видеть, что мы формируем с его помощью строку, которая будет содержать текст вида "(<значение X точки>; <значение Y точки>)" и передаём координаты точки point, которую метод принимает в своих параметрах.
Далее мы создаём переменную mouseCursorCoordinatesFont и записываем в неё новый экземпляр шрифта с заданными параметрами.
Затем мы в переменную textSize записываем результат вызова метода MeasureString, который измеряет прямоугольник, в который будет встроена строка текста, учитывая саму строку текста (т.е. её содержимое) и шрифт, которым она будет рисоваться на форме. Этот размер нам поможет далее нарисовать фоновый прямоугольник на фоне текста, цвет этого прямоугольника будет совпадать с цветом фона нашей формы (свойство формы BackColor).
Далее мы создаём переменную bgColorForBrush, в которую записываем результат создания экземпляра цвета (стандартная структура Color), а сам цвет при помощи вызова метода FromArgb мы создаём через указание 4-х аргументов: 1-й аргумент, равный 210, задаёт Alpha-канал. Доступные значения параметра от 0 до 255. Если значение равно 255, то цвет будет полностью непрозрачным, т.е. сплошным. В нашем же случае мы передаём значение 210, что позволяет целевому цвету быть слегка прозрачным. В остальных трёх аргументах мы передаём 3 компонента цвета (R - Red, красный; G - Green, зелёный; B - Blue, синий), который берём с текущего значения свойства фона для нашей формы - BackColor.
Сразу после этого мы создаём экземпляр кисти для отрисовки фона для текста и записываем эту кисть в переменную brushForTextBackground.
Следом идут 2 строки, где мы рисуем фон для текста, вызывая метод GDI+ FillRectangle, а также метод DrawString для отрисовки нашей строки с координатами. обратите внимание, что относительно переданной точки point мы делаем небольшое смещение текста вправо-вверх: за счёт отнятия 5 пикселей от координаты X и 25 пикселей от координаты Y точки point.
В самом конце перед выходом из метода, мы должны не забыть подчистить занятые ресурсы - освободить их для созданного экземпляра шрифта mouseCursorCoordinatesFont и экземпляра кисти brushForTextBackground, вызвав у них метод Dispose().
Ещё нам потребуется два перегруженных метода с таким же именем, давайте добавим их также в код формы:
private void DrawCoordinatesForPoint(Graphics g, PointF point) {
DrawCoordinatesForPoint(g, point, Brushes.Green);
}
private void DrawCoordinatesForPoint(Graphics g, Point point) {
DrawCoordinatesForPoint(g, new PointF(point.X, point.Y));
}Они нужны для того, чтобы можно было рисовать координаты некоторым стандартным для нашей программы-примера цветом (при помощи зелёной кисти Brushes.Green), а также использовать вместо экземпляра структуры Point другую структуру PointF. Различие PointF от Point в том, что у PointF координаты задаются как значения типа данных float, а у Point - как значения типа данных int. Т.е. введя эти перегруженные методы мы также сможем передавать в наш метод DrawCoordinatesForPoint экземпляр точки в виде структуры PointF, это нам пригодится далее.
Теперь напишем следующий метод DrawResetTextHint(Graphics g), который после отрисовки линии выведет строку текста "Клик правой кнопкой мыши - сброс измерений и начать заново" на главной форме:
/// <summary>
/// Выводит текст "Клик правой кнопкой мыши - сброс измерений и начать заново", когда линия уже нарисована
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки текста</param>
private void DrawResetTextHint(Graphics g) {
Font fontForHint = new Font("Arial", 14, FontStyle.Bold);
string hint = "Клик правой кнопкой мыши - сброс измерений и начать заново";
SizeF hintTextSize = g.MeasureString(hint, fontForHint);
g.DrawString(hint, fontForHint, Brushes.Purple, new PointF(Width / 2 - hintTextSize.Width / 2, Height - hintTextSize.Height - 100));
fontForHint.Dispose();
}Здесь должно быть уже всё понятно, поскольку для вывода текста мы используем ту же механику, что использовали ранее для вывода координат: определяем экземпляр шрифта, задаём строку, измеряем её размеры при помощи вызова метода MeasureString, доступного в классе Graphics, затем выводим строку при помощи метода DrawString, который также есть в классе Graphics. Напоследок мы очищаем ресурсы, занимаемые экземпляром шрифта.
Теперь мы напишем ещё один метод DrawLineCentralPoint(Graphics g, PointF lineCentralPoint, bool isEstimateCentralPoint), который будет рисовать на форме центральную точку для линии. Отрисовка центральной точки будет осуществляться либо в виде окружности (когда мы находимся в режиме выбора 2-й точки линии), либо в виде закрашенного круга (когда линия полностью отрисована и обе точки линии известны). Код метода представлен ниже:
/// <summary>
/// Метод рисует центральную точку <paramref name="lineCentralPoint"/>.
/// В зависимости от значения параметра <paramref name="isEstimateCentralPoint"/> центральная точка рисуется либо
/// в виде окружности (когда параметр <paramref name="isEstimateCentralPoint"/> равен true), либо в виде
/// закрашенного круга (когда параметр <paramref name="isEstimateCentralPoint"/> равен false).
/// </summary>
/// <param name="g">экземпляр класса Graphics для отрисовки центральной точки линии</param>
/// <param name="lineCentralPoint">задаёт центральную точку линии</param>
/// <param name="isEstimateCentralPoint">задаёт режим отрисовки центральной точки. Если параметр равен true, будет нарисована окружность, иначе - будет нарисован круг</param>
private void DrawLineCentralPoint(Graphics g, PointF lineCentralPoint, bool isEstimateCentralPoint) {
PointF circleTopLeftCornerForLineCentralPoint = lineCentralPoint - new SizeF(5, 5);
if (isEstimateCentralPoint) {
g.DrawEllipse(Pens.Orange, new RectangleF(circleTopLeftCornerForLineCentralPoint, new SizeF(10, 10)));
} else {
g.FillEllipse(Brushes.Orange, new RectangleF(circleTopLeftCornerForLineCentralPoint, new SizeF(10, 10)));
}
}В первой строке метода вычисляются координаты левого-верхнего угла квадрата размером 10x10 пикселей, описанного вокруг окружности/круга, который представляют центральную точку линии. Если входной параметр метода isEstimateCentralPoint будет равен true, то мы будем рисовать окружность с оранжевым цветом контура (Pens.Orange), в противном случае мы будем рисовать круг, залитый при помощи оранжевой кисти (Brushes.Orange).
Теперь нам осталось написать последний вспомогательный метод GetLineCentralPoint(Point first, Point second), который будет вычислять центральную точку линии и должен возвращать экземпляр структуры PointF. Этот метод будет одним из ключевых во всей нашей программе, поскольку его задача - определить местоположение центральной точки линии. И в этом нам как раз помогут знания тригонометрических функций, а также знаменитая теорема Пифагора. Как именно помогут? Мы узнаем уже в следующем разделе, поскольку для понимания расчёта центральной точки линии нам потребуется немного погрузиться в алгоритм нахождения центральной точки и вспомнить некоторые аспекты из курса средней школы и посмотреть на иллюстрации, демонстрирующие тонкости нахождения центральной точки.
Вычисляем местоположение центральной точки линии при помощи теоремы Пифагора и тригонометрической функции Cos ("косинус")
Ниже мы рассмотрим возможные варианты расположения двух точек линии относительно друг друга. Рассмотрим первый случай, когда точка P2 лежит правее-ниже точки P1. Пусть P1(x1; y1) - это первая точка нашей линии, а P2(x2; y2) - это потенциальная вторая точка линии (и она же - местоположение курсора мыши на момент выбора в нашей программе 2-й точки линии). Давайте построим на двух точках P1 и P2 нашей линии прямоугольный треугольник и на его гипотенузе c, которая и является фактически нашей рисуемой линией, мы отметим центр гипотенузы - точку M(Xmed; Ymed). Эта точка и есть центр нашей рисуемой линии, но она одновременно является и второй точкой медианы m, проведённой к гипотенузе из прямого угла треугольника (см. рисунок ниже):
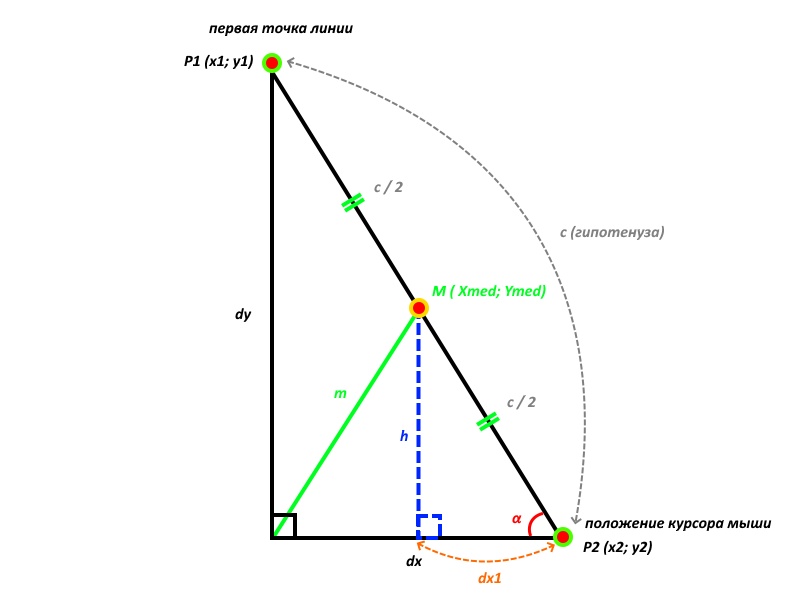
Рис. 1. Точка P2(x2; y2) находится правее-ниже точки P1(x1; y1)
Наша задача заключается в том, чтобы определить местоположение точки M(Xmed; Ymed) и вычислить её координаты Xmed и Ymed.
Для решения этой задачи мы проведём из точки M к нижнему катету нашего прямоугольного треугольника высоту h (на рисунке отмечена синим цветом). Мы также отметим правый нижний угол нашего треугольника как α ("альфа"). На рисунке можно видеть, что этот угол α также является углом маленького вложенного прямоугольного треугольника, который образовался после проведения высоты h к основанию нашего большого (основного) треугольника. Точка, в которой высота h пересекается с нижним катетом основного треугольника, определяет расстояние dx1 до точки P2(x2; y2). Вместе с этим, dx1 - это также и нижний катет маленького (внутреннего) прямоугольного треугольника, это понимание нам пригодится чуть далее.
По рисунку становится понятно, что для определения координат точки M мы должны по сути вычислить высоту h и это расстояние dx1, поскольку, зная эти величины, мы без труда найдём координаты Xmed и Ymed по следующим формулам:
- Xmed = x2 - dx1 (1)
- Ymed = y2 - h (2)
Давайте теперь поймем, какие данные из тех, что отражены на рисунке, у нас уже имеются или какие из них мы можем вычислить по имеющимся данным? Мы знаем координаты точек P1 и P2, следовательно, мы можем рассчитать расстояния dx и dy, которые являются катетами большого прямоугольного треугольника. Давайте вычислим их:
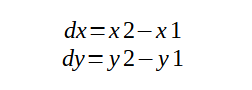
Теперь нам нужно вычислить гипотенузу c по теореме Пифагора (для тех, кто подзабыл, теорема звучит так: "квадрат гипотенузы равен сумме квадратов катетов", соответственно, для нахождения гипотенузы c нам нужно извлечь квадратный корень из суммы квадратов катетов): 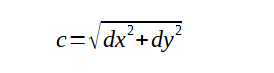
Зная величину гипотенузы c мы также легко вычисляем её половину с / 2, которая, в свою очередь, также является величиной, равной гипотенузе для маленького вложенного прямоугольника, у которого катеты равны h и dx1.
Далее, чтобы вычислить искомые величины h и dx1 нам необходимо знать значение cos α, т.е. величину косинуса угла "альфа". Косинус, из курса тригонометрии, - это отношение прилегающего к углу катета (dx) к гипотенузе (c). Обратим также внимание, что этот угол - общий как для большого треугольника, так и для маленького, вложенного.
Рассчитаем cos α по большому треугольнику, то есть как отношение катета dx к гипотенузе c:
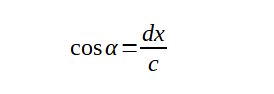
В свою очередь, поскольку угол α - общий для обоих треугольников, мы можем его выразить и как соотношение катета маленького треугольника к его гипотенузе:
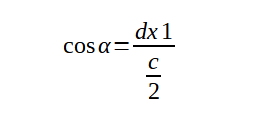
Исходя из этого, приравняв правые части двух предыдущих выражений для cos α, мы получаем следующее равенство:
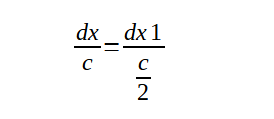
В нём нам уже известны все величины, кроме искомой dx1, поэтому осталось вычислить dx1:

или, если упростить произведение в правой части и убрать теперь c:
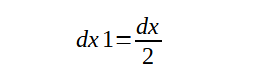
Таким образом, величина dx1 равна половине dx.
Осталось вычислить высоту h по той же теореме Пифагора. Поскольку h - это больший из катетов маленького вложенного треугольника, то нам нужно взять квадратный корень из вычитания квадрата dx1 из квадрата половины гипотенузы:
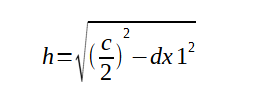
Итак, мы успешно нашли искомые величины h и dx1, а значит, сможем рассчитать по формулам (1) и (2) и координаты центральной точки M для нашей линии, соединяющей точки P1 и P2.
Но сейчас мы рассмотрели только один вариант, когда точка P2 лежит правее-ниже точки P1. Как быть с другими случаями?
Давайте рассмотрим и их и поймем, что все основные расчёты, что мы уже выполнили, нам пригодятся и в остальных случаях.
Итак, если точка P2 лежит левее-ниже точки P1, мы получим следующую картину:
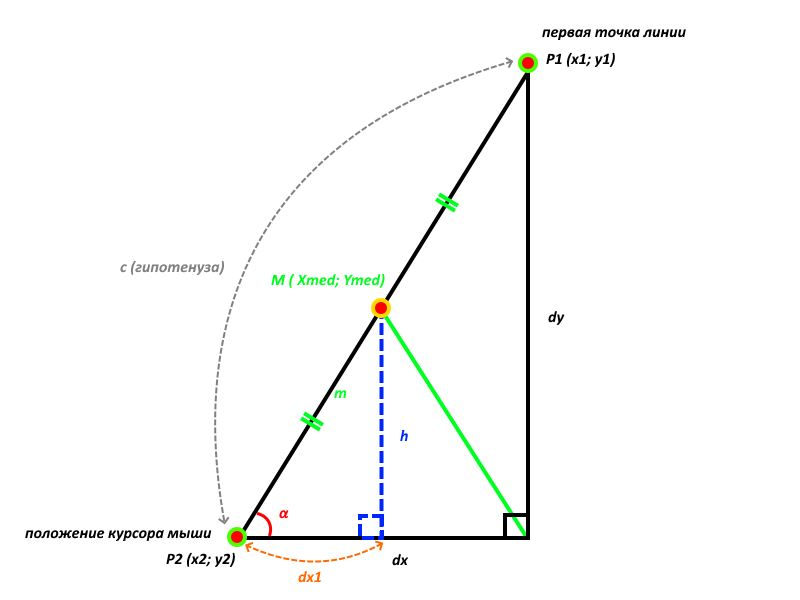
Рис. 2. Точка P2(x2; y2) находится левее-ниже точки P1(x1; y1)
Если точка P2 лежит левее-выше точки P1, то картина будет следующей:
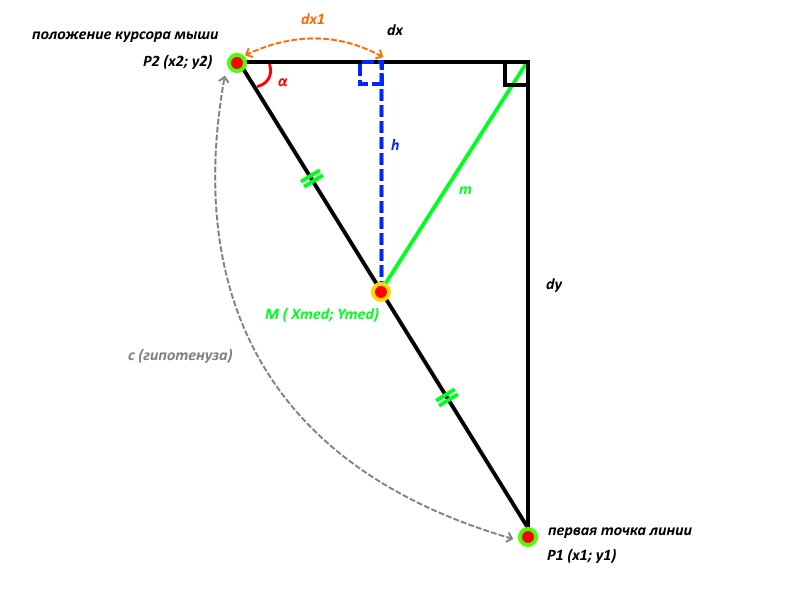
Рис. 3. Точка P2(x2; y2) находится левее-выше точки P1(x1; y1)
Наконец, если точка P2 лежит правее-выше точки P1, то мы получим следующую картину:
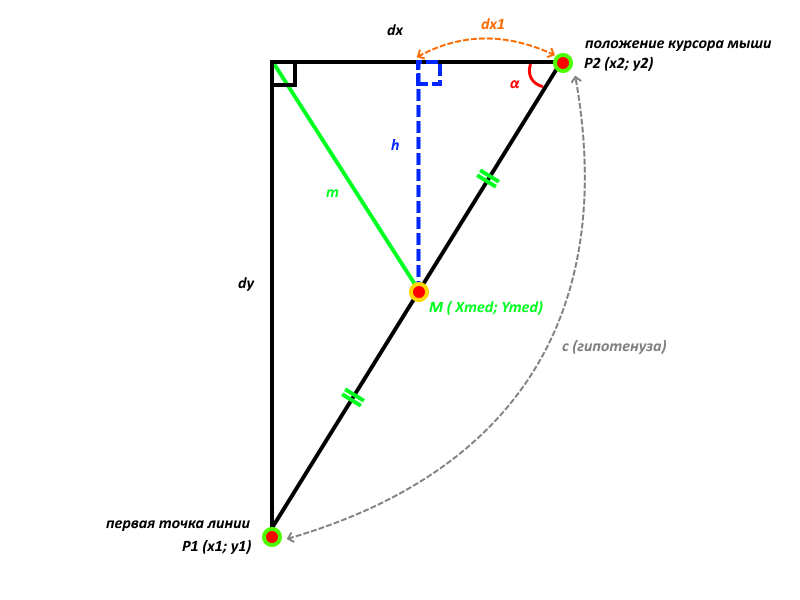
Рис. 4. Точка P2(x2; y2) находится правее-выше точки P1(x1; y1)
Можно обратить внимание на то, что является общим, а что будет отличаться в представленных ситуациях, в зависимости от взаимного расположения точек P1, P2:
- все расстояния, включая искомые dx1 и h, а также взаимное расположение высоты h, катета dx1 и угла α являются одинаковыми во всех описанных ситуациях. Это означает, что dx1 и h равны во всех случаях.
- отличным будет механизм вычисления координат Xmed и Ymed для центральной точки M, т.е. будут отличны формулы (1) и (2), что мы определили при первом расчёте. Во всех случаях мы будем вычислять эти координаты, отталкиваясь от точки P2 и её координат x2, y2. Но делать это вычисление будем, глядя на представленные выше рисунки.
Ниже приведём сразу расчёт координат Xmed и Ymed по каждому из четырёх случаев:
- Случай 1 и рисунок 1: Точка P2(x2; y2) находится правее-ниже точки P1(x1; y1). Формулы (1) и (2) мы уже вывели:
- Xmed = x2 - dx1
- Ymed = y2 - h
- Случай 2 и рисунок 2: Точка P2(x2; y2) находится левее-ниже точки P1(x1; y1). Формулы (1) и (2) будут следующими:
- Xmed = x2 + dx1
- Ymed = y2 - h
- Случай 3 и рисунок 3: Точка P2(x2; y2) находится левее-выше точки P1(x1; y1). Формулы (1) и (2) будут следующими:
- Xmed = x2 + dx1
- Ymed = y2 + h
- Случай 4 и рисунок 4: Точка P2(x2; y2) находится правее-выше точки P1(x1; y1). Формулы (1) и (2) будут следующими:
- Xmed = x2 - dx1
- Ymed = y2 + h
Мы рассмотрели те 4 случая, когда координаты X и Y у точек P1 и P2 отличны. Но что если эти точки лежат на какой-то одной прямой, параллельной оси X или параллельной оси Y? Здесь у нас также может быть 4 возможных случая, но во всех этих случаях нам уже не нужна будет теорема Пифагора и тригонометрическая функция косинуса, поскольку будет достаточно либо от координаты Y какой-то одной из точек отнять величину dy/2, либо от координаты X какой-то одной из точек отнять величину dx/2, ведь dy и dx - это уже расстояния между точками по соответствующей оси.
Остался последний (вырожденный) случай - когда точки P1 и P2 полностью совпадают и представляют собой одну и ту же точку с какими-то координатами. Но в этом случае и центральная точка такой линии с нулевой длиной будет совпадать с точками P1 и P2.
Учитывая все детали, что мы рассмотрели выше, мы готовы написать реализацию метода, вычисляющего центральную точку линии во всех возможных комбинациях расположения точек P1 и P2. Один важный момент - при вычислении dx, dy мы возьмем абсолютное значение разницы между соответствующими координатами точек, чтобы не допустить возникновения отрицательных значений.
Добавим в код главной формы метод GetLineCentralPoint(Point first, Point second):
/// <summary>
/// Метод вычисляет центральную точку линии (отрезка, заключённого между точками <paramref name="first"/> и <paramref name="second"/>).
/// </summary>
/// <param name="first">Первая точка линии</param>
/// <param name="second">Вторая точка линии</param>
/// <returns>Экземпляр структуры PointF, содержащий координаты центральной точки линии</returns>
private PointF GetLineCentralPoint(Point first, Point second) {
if (first.X == second.X && first.Y == second.Y) {
// Если точки first и second полностью совпадают по координатам, то и центральная точка - совпадает с ними
return new PointF(first.X, first.Y);
}
double dx = Math.Abs(second.X - first.X);
double dy = Math.Abs(second.Y - first.Y);
if (first.X == second.X) {
// Первая и вторая точка линии лежат на одной вертикали
if (first.Y > second.Y) {
return new PointF(first.X, first.Y - (float)(dy / 2));
} else {
return new PointF(second.X, second.Y - (float)(dy / 2));
}
} else if (first.Y == second.Y) {
// Первая и вторая точка линии лежат на одной горизонтали
if (first.X > second.X) {
return new PointF(first.X - (float)(dx / 2), first.Y);
} else {
return new PointF(second.X - (float)(dx / 2), second.Y);
}
}
// Вычисляем по теореме Пифагора длину гипотенузы большого прямоугольного треугольника
double c = Math.Sqrt(Math.Pow(dx, 2) + Math.Pow(dy, 2));
// Проверяем отдельно, что гипотенуза точно не равна 0 и не является специальным значением (NaN, Infinity).
// Эту проверку, в целом, можно убрать, поскольку вырожденный случай, когда точки first и second являются одной и той же
// точкой, мы уже проверили в самом начале. И, если это и произошло, то мы уже вернёмся из метода там, вернув new PointF(first.X, first.Y).
if (c == 0 || double.IsNaN(c) || double.IsInfinity(c)) {
return PointF.Empty;
}
// Вычисляем половину длины гипотенузы
double halfOfHypotenuse = c / 2;
// Вычисляем dx1
double dx1 = dx / 2;
// Вычисляем по теореме Пифагора высоту h маленького треугольника.
// halfOfHypotenuse^2 = h^2 + dx1^2 => h = Math.Sqrt( halfOfHypotenuse^2 - dx1^2 )
double h = Math.Sqrt(Math.Pow(halfOfHypotenuse, 2) - Math.Pow(dx1, 2));
PointF lineCentralPoint;
if (second.Y > first.Y && second.X > first.X) {
// Случай 1. Вторая точка - правее-ниже первой точки
lineCentralPoint = new PointF((float)(second.X - dx1), (float)(second.Y - h));
} else if (second.Y > first.Y && second.X < first.X) {
// Случай 2. Вторая точка - левее-ниже первой точки
lineCentralPoint = new PointF((float)(second.X + dx1), (float)(second.Y - h));
} else if (second.Y < first.Y && second.X < first.X) {
// Случай 3. Вторая точка - левее-выше первой точки
lineCentralPoint = new PointF((float)(second.X + dx1), (float)(second.Y + h));
} else if (second.Y < first.Y && second.X > first.X) {
// Случай 4. Вторая точка - правее-выше первой точки
lineCentralPoint = new PointF((float)(second.X - dx1), (float)(second.Y + h));
} else {
// Мы не должны попадать сюда никогда, но даже если и попали, то на выходе из метода будет
// всегда экземпляр пустой точки (её координаты 0; 0)
return PointF.Empty;
}
return lineCentralPoint;
}Код этого метода, во-первых и так снабжён комментариями, а во-вторых, мы провели подготовительную работу и на рисунках разобрали, как он должен вычислять центральную точку линии, поэтому в дополнительных пояснениях не нуждается. Лишь отмечу, что мы в коде метода использовали стандартный класс System.Math из .NET Framework, который представляет нужные нам функции для извлечения квадратного корня (Math.Sqrt) и возведения аргумента в нужную степень (Math.Pow).
Финальные шаги. Доработка метода-обработчика для события Paint
Друзья, мы уже написали все вспомогательные методы для работы нашей программы, включая метод по расчёту центральной точки линии, и теперь нам лишь осталось вернуться к методу-обработчику события Paint и заменить в нём TODO-комментарии на полезные вызовы наших вспомогательных методов, чтобы "оживить" нашу программу:
Доработаем наш метод-обработчик для события Paint следующим образом:
private void FrmFindCenterOfLine_Paint(object sender, PaintEventArgs e) {
Graphics g = e.Graphics;
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.HighQuality;
// Получим координаты курсора мыши в клиентских координатах
Point mouseCursorPositionClient = GetMouseCursorPositionInClientCoordinates();
PointF lineCentralPoint;
switch (CurrentLinePaintingState) {
case LinePaintingState.ChoosingFirstPoint:
// рисуем окружность около текущего местоположения курсора мыши
DrawCircleForMouseCursor(g, mouseCursorPositionClient);
// отрисовываем координаты текущего местоположения курсора мыши
DrawCoordinatesForPoint(g, mouseCursorPositionClient);
break;
case LinePaintingState.ChoosingSecondPoint:
// рисуем пунктирную линию от 1-й точки до текущего местоположения курсора мыши
DrawLineFromFirstPointToOtherPoint(g, GetMouseCursorPositionInClientCoordinates());
// отрисовываем 1-ю точку линии
DrawLinePoint(g, FirstLinePoint, Brushes.Red);
// рисуем окружность около текущего местоположения курсора мыши
DrawCircleForMouseCursor(g, mouseCursorPositionClient);
// получаем центральную точку линии
lineCentralPoint = GetLineCentralPoint(FirstLinePoint, mouseCursorPositionClient);
// рисуем центральную точку текущей выбираемой линии
DrawLineCentralPoint(g, lineCentralPoint, true);
// отрисовываем координаты центральной точки
DrawCoordinatesForPoint(g, lineCentralPoint, Brushes.Orange);
// отрисовываем координаты 1-й точки
DrawCoordinatesForPoint(g, FirstLinePoint);
// отрисовываем координаты текущего местоположения курсора мыши
DrawCoordinatesForPoint(g, mouseCursorPositionClient);
break;
case LinePaintingState.WaitingForReset:
// рисуем пунктирную линию от 1-й точки до 2-й точки
DrawLineFromFirstPointToOtherPoint(g, SecondLinePoint);
// отрисовываем 1-ю точку линии
DrawLinePoint(g, FirstLinePoint, Brushes.Red);
// отрисовываем координаты 1-й точки
DrawCoordinatesForPoint(g, FirstLinePoint);
// отрисовываем 2-ю точку линии
DrawLinePoint(g, SecondLinePoint, Brushes.Blue);
// отрисовываем координаты 2-й точки
DrawCoordinatesForPoint(g, SecondLinePoint);
// получаем центральную точку линии
lineCentralPoint = GetLineCentralPoint(FirstLinePoint, SecondLinePoint);
// рисуем центральную точку (не в режиме эскиза) для текущей линии
DrawLineCentralPoint(g, lineCentralPoint, false);
// отрисовываем координаты центральной точки
DrawCoordinatesForPoint(g, lineCentralPoint, Brushes.Orange);
// выводим текст на форме с подсказкой о том, что правый клик мыши сбросит все измерения
DrawResetTextHint(g);
break;
}
}Я позволил себе снабдить комментариями все новые строки кода, добавленные вместо TODO-комментариев, что мы добавили ранее в качестве "заглушек". Хоть это и не самая лучшая практика - подобным образом и настолько детально комментировать код прямо внутри метода, я преследовал цель пояснить всем читателям каждый происходящий шаг.
Отмечу лишь один нюанс, который важен для понимания последовательности расположения наших вспомогательных методов в каждой из case-развилок: порядок методов в каждой развилке должен быть таким, чтобы учитывать последовательность прорисовки фигур: т.е. фигуры, которые далее могут "перекрываться" (полностью или частично - не столь важно) другими рисуемыми фигурами, должны быть нарисованы раньше, чем остальные. А значит, вызов вспомогательного метода, их рисующего, также должен располагаться раньше вызовов остальных вспомогательных методов.
Теперь мы полностью завершили работу над проектом, все методы нашей программы написаны и готовы. Можно запустить приложение, нажав F5 или кнопку "Пуск" на панели инструментов среды разработки и проверить его работу.
Как я и обещал, ссылка на архив с готовым примером, что мы только что разработали:
На этом всё, спасибо за внимание. Делитесь мыслями и вопросами в комментариях и не забудьте поставить лайк вверху статьи, если она вам пригодилась и понравилась.

